Lange und kurze Arme
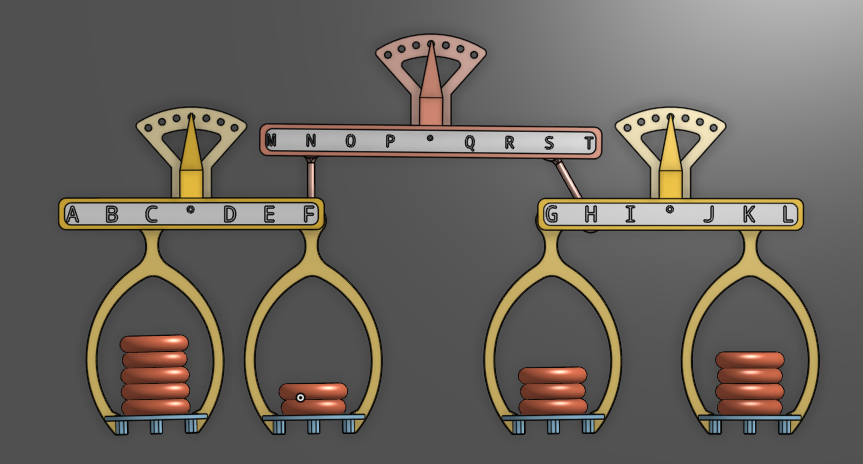
Beide Waagen sind im Gleichgewicht, also steht auch der rote Balken waagrecht. Die Hebelarme (N,O) sind gleich lang. Beobachte die rote Skala, wenn du entweder bei A oder bei K einen Würfel dazu legst.
Der Ausschlag geht natürlich einmal nach links und einmal nach rechts. Aber er ist auch unterschiedlich groß! Warum?
Die Ausschläge aller Zeiger sind gleich groß, wenn ein Würfel auf A oder K liegt, weil F,N,O,G gleich weit von ihren Achsen entfernt sind. Allerdings reagieren die Zeiger schwächer, wenn der Zusatzwürfel bei K aufgelegt wird. Ursache ist, dass die Gewichte der rechten Waage näher an der Achse sitzen. Wie so oft, hilft es auch hier, sich eine Extremsituation vorzustellen. Würden die Waagschalen rechts beide genau hintereinander auf der Achse des Waagbalkens sitzen (also in der Mitte zwischen I und J), dann hätten sie gar keine Wirkung auf den mittleren Balken!
Der kleine Hebel sitzt woanders
Für das Gleichgewicht macht es keinen Unterschied, wo der kleine rote Hebel auf der rechten Seite sitzt.
Lege auch jetzt wieder abwechselnd einen Zusatzwürfel bei A oder bei K auf. Beobachte die gelben und die roten Skalen. Vergleiche die Ausschläge mit denjenigen der vorherigen Aufgabe. Kannst du erklären, warum sie verschieden sind?
Die Ausschläge auf den gelben Skalen sind jetzt nicht mehr gleich groß, denn P bewegt sich grundsätzlich immer weiter weg von der Horizontalen als N. Da H näher an seiner Achse sitzt als F, wird dieser Effekt noch verstärkt.
Die rechte Waage reagiert daher diesmal insgesamt stärker als die linke, obwohl ihre Waagschalen näher an der Mitte hängen. Aber über H und P übt sie eine doppelt so große Wirkung auf die linke Waage aus. 2 * 2 / 3 ist mehr als 1, also hat sie stärkeren Einfluss auf die Gesamtsituation.
Drei Waagschalen
Linke Waage: 9 – 3; rechte Waage = 6; Gleichgewicht!
Wenn sich kein genaues Gleichgewicht einstellt, liegt es daran, dass die Holzwürfel nicht exakt dasselbe Gewicht haben. Wenn man sie ein wenig herumtauscht, stellt sich das Gleichgewicht ein.
Bei F sieht man eine kleine gelbe Scheibe auf dem Waagteller. Sie sorgt zusammen mit einer nicht sichtbaren Metallplatte, die am Teller mit der Nummer 2 befestigt ist, dafür, dass die Waage im Gleichgewicht ist, wenn alle Teller leer sind.
Drei Schalen mit längerem Hebel rechts
4 * 3 = 3 * 4
Drei Hebel, 2:1
Aufgabe: Baue die Waagen so um, dass es nur zwei Waagschalen gibt, aber drei Waagbalken. Wir wollen, dass Gleichgewicht herrscht, wenn auf der linken Waage doppelt so viel Würfel liegen wie auf der rechten.
Die Schüler spüren, dass die Ausschläge bei Gewichtsunterschieden kleiner sind. Die Waage ist weniger empfindlich, weil die Wirkungen wegen der kurzen Hebelarme links und rechts außen klein sind.
Der mittlere Arm ist zwar lang, aber er überträgt nur die Wirkungen, welche die beiden äußeren Waagen erzeugen.
Wenn wir links und rechts nur einen Würfel auflegen, gerät die Waage in große Schieflage. Sie verklemmt sich sogar so , dass wir sie nur mit viel Gefühl wieder in einen normalen Zustand zurück versetzen können. Je nach dem Schwung, den sie bekommt, kann der rote Hebel links sogar einen Überschlag machen und dann in die falsche Richtung zeigen.
Wir sollten den Schülern diese Erfahrung nicht vorenthalten!
Ein Hebel steht schräg
Links wirken 5G * 1A = 5W gegen 2G * 3A = 6W. (DEF) = 1W.
Rechts sind es 4G * 2A = 8W gegen 3G * 3A = 9W. (GHI) = 1W.
Mittelbalken links: 1W (DEF) / 3A (F) * 3A (N) ergibt 1W (MNOP)
Mittelbalken rechts: 1W (GHI) / 2A (H) * 3A (S) ergibt 1.5 W (QRST).
Aber die Kraft bei H wirkt nur anteilig auf (S), weil der kleine Hebel schräg steht. Wenn das Konzept der Winkelfunktionen bekannt ist, kann man auf den Cosinus verweisen. Der Winkel zwischen dem rechten Kopplungshebel und der Senkrechten beträgt etwa 30°, d.h. der Cosinus ist ~ 0.87. Rechts wirkt auf den mittleren Hebel abwärts also eine Kraft von 1.5 * 0.87 ~ 1.3. Bei ca. 49° Winkel wäre der Cosinus ~ 2/3. Dann würde die resultierende Kraft rechts ebenfalls 1 ergeben und wir hätten perfektes Gleichgewicht.
Jüngere Kinder können durchaus intuitiv erfassen, dass ein Hebel, an dem man schräg zieht, eine geringere Wirkung auf den mittleren Balken hat als einer, der senkrecht steht. Stellt euch mal vor, der rechte Hebel wäre sehr lang und würde fast ganz waagrecht liegen, weil die rechte Waage weit draußen auf der rechten Seite montiert wäre. Da würde der meiste Teil der Kraft nur an der Befestigung der Achse ziehen, hätte aber keine Wirkung auf den Balken.
Eine andere Art der intuitiv verstehbaren Begründung könnte so lauten: Wenn der rechte Hebel nach oben zeigen würde, hätte er genau die gegenteilige Wirkung, wie wenn er nach unten zieht (Minus / Plus). Wenn er in der Mittelposition steht, also genau waagrecht, dann ist seine Wirkung 0. Je mehr er von der Senkrechten abweicht (schief steht), desto kleiner ist seine anteilige Wirkung auf den Balken.
Blockierte Waage

Links 3 * 4, rechts 6 *2. Das ergibt 12 auf beiden Seiten. Klarer Fall von Gleichgewicht!
Wirklich? Die Kraft bei F zieht nach unten, die Kraft bei G drückt aber nach oben. Warum steht der mittlere Balken nicht total schräg?
Weil er blockiert ist! Die vier Hebel bilden eine „Verspannung“ (ein Tragwerk), d.h. keiner der Waagbalken kann sich irgendwie bewegen! Man könnte überall beliebige Gewichte auflegen, ohne dass sich etwas verändert.
Extreme Verhältnisse
(DEF) = 2 – 0 = 2; die Kraft der linken Waage drückt von F (Abstand 3) nach schräg rechts oben zu „:“ (Abstand = 2), der mittlere Balken drückt von P (Abstand 4) schräg nach rechts unten zu I. Von C aus gesehen haben wir ein Übersetzungsverhältnis von 3:1 mal 0,87 mal 2:1 mal 0,87 bis zu I, also 6 * 0.75 : 1 = 8 : 1. Ein Würfel, den wir links bei C auflegen, wirkt also bei I so wie 1/8 Würfel.
echte Waage drückt von I (Abstand 1) nach oben zu P (Abstand 4). Sind die Wirkungen gleich groß?
Wir rechnen: 2 / 3 * 2 = 4/3 (links) und 1 / 1 * 4 = 4 (rechts).
Das ergibt einen deutlichen Unterschied, der mittlere Balken hebt sich also rechts, weil dort die nach oben drückende Kraft größer ist als rechts.
Wir beobachten, dass sich die Waage nur sehr geringfügig bewegt, wenn man bei C Würfel dazu legt. Man kann es auch spüren, wenn man mit dem Finger drückt. Wir haben ein Übersetzungsverhältnis von 3 : 1 am linken Waagbalken und 2:1 am mittleren, d.h. jeder Würfel, den wir bei C auflegen, wirkt nur mit 1 / 6 seines Gewichts bei P.
Weihnachtsmarkt
Hier noch ein hübsches Rätsel von Ingmar Rubin (Berlin):

Auf einem Weihnachtsmarkt fand ich einen Verkaufsstand, an dem diverse Köstlichkeiten angeboten wurden, als da wären: gebrannte Mandeln, feinste Schokostreusel, türkischer Honigkuchen und kandierte Apfel. So war es kein Wunder, dass vor allem die kleinen Kinder mit laufenden Nasen und leuchtenden Augen an diesem Stand ein großes Gedränge verursachten. Und dies war wohl auch der entscheidende Grund für das Malheur: Irgendwann schepperte es, und die stilvolle Balkenwaage zum Abwiegen des Süßkrams lag samt dem dazu gehörenden Satz an Wägestücken auf dem Boden. Die Wägestücke sind durch den Sturz nicht beschädigt worden, wohl aber war der Waagebalken verrutscht, so dass die Arme der Balkenwaage nicht mehr die gleiche Länge aufwiesen.
Der Verkäufer hatte aber sofort einen Ausweg aus diesem Dilemma parat:
Er wog bei jedem Kunden zweimal ab, indem er eine Hälfte des gewünschten Süßwerks auf der linken Waagschale mit dem entsprechenden Wägestück auf der rechten Schale gegengewogen hat und anschließend umgekehrt.
Wünschte also beispielsweise jemand 500 Gramm gebrannte Mandeln, so wurden zunächst auf der linken Schale 250 Gramm abgewogen (das 250-Gramm-Wägestück lag dabei auf der rechten Schale) und anschließend 250 Gramm auf der rechten Schale (das 250-Gramm-Wägestück lag dabei auf der linken Schale).
Was ich mich nun frage, ist, ob damit der Fehler der Waage tatsächlich ausgeglichen wird oder nicht?
- Der Fehler wird durch das zweimalige Wiegen vollständig ausgeglichen.
- Der Kunde erhält stets mehr als die gewünschte Menge.
- Der Kunde bekommt auf diese Weise immer 9/8 des verlangten Gewichtes.
- Der Kunde erhält stets weniger als die gewünschte Menge.
- Die Frage lässt sich nur genau beantworten, wenn man ausmessen kann, um wie viele Millimeter der Waagebalken aus der Mitte verschoben ist.
- Das Verfahren funktioniert nur bei einer Menge von 500 Gramm exakt.
- Der Kunde bekommt auf diese Weise stets die doppelte Menge an Süßwaren.
- Der Kunde bekommt auf diese Weise stets die halbe Menge an Süßwaren.
- Es gibt genau drei mögliche Positionen des Waagbalkens, so dass die Balkenwaage exakt misst.
- Man erhält stets mehr als die gewünschte Menge, aber nicht mehr als das Doppelte.